Dirichlet BC and Nodal Source Term
Equations
We solve the Poisson equation:
$$ \begin{equation} k\\;\Delta h = f(x) \quad \text{in }\Omega \end{equation}$$w.r.t boundary conditions
$$ \eqalign{ h(x) = g_D(x) &\quad \text{on }\Gamma_D,\cr k\\;{\partial h(x) \over \partial n} = g_N(x) &\quad \text{on }\Gamma_N, }$$where $h$ could be hydraulic head, the subscripts $D$ and $N$ denote the Dirichlet- and Neumann-type boundary conditions, $n$ is the normal vector pointing outside of $\Omega$, and $\Gamma = \Gamma_D \cup \Gamma_N$ and $\Gamma_D \cap \Gamma_N = \emptyset$.
Problem specification and analytical solution
We solve the Poisson equation on a circle domain with radius $r = 1$ with $k = 1$ w.r.t. the specific boundary conditions:
$$ \eqalign{ h(x,y) = 0 &\quad \text{on } (x^2 + y^2 = 1) \subset \Gamma_D,\cr }$$The solution of this problem is
$$ h(x,y) = \int \int f(\xi, \eta) G(x, y) d \xi d \eta, $$where $G(x, y)$ is the Green’s function. For the example at hand $G(x, y)$ is:
$$ G(x, y) = \frac{1}{2 \pi} \ln \sqrt{(x-\xi)^2 + (y-\eta)^2}. $$With a nodal source term of 1 at $(0.0, 0.0)$ the analytical solution is
$$ h(x,y) = \frac{1}{2 \pi} \ln \sqrt{x^2 + y^2}. $$Input files
The main project file is square_1e6_with_nodal_sources.prj. It describes the process to be solved and the related process variables together with their initial and boundary conditions as well as the definition of the nodal source term. It also references the mesh and geometrical objects defined on the mesh.
The geometries used to specify the boundary conditions and the source term are given in the square_1x1.gml file.
The input mesh square_1x1_quad_1e6.vtu is stored in the VTK file format and can be directly visualized in ParaView for example.
Running simulation
To start the simulation (after successful compilation) run:
ogs circle_1e6_axi.prjIt will produce some output and write the computed result into a data array of the written VTU file.
Results and evaluation
Comparison of the analytical solution and the computed solution
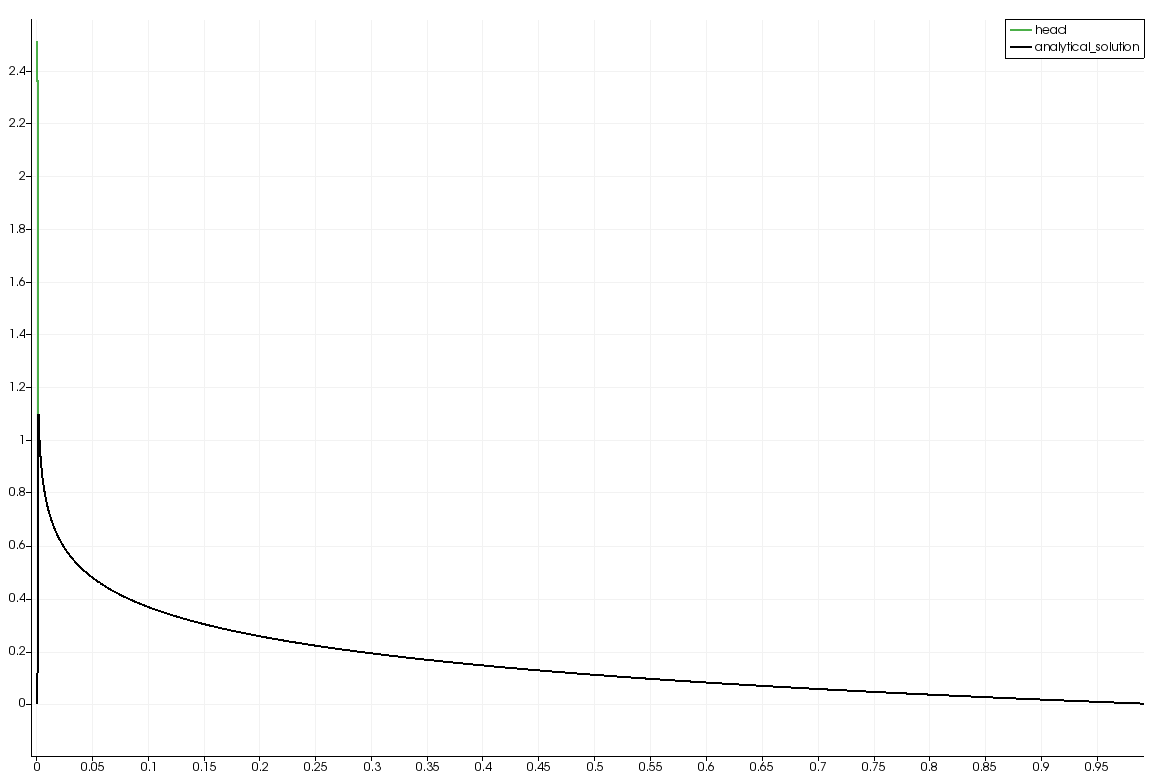
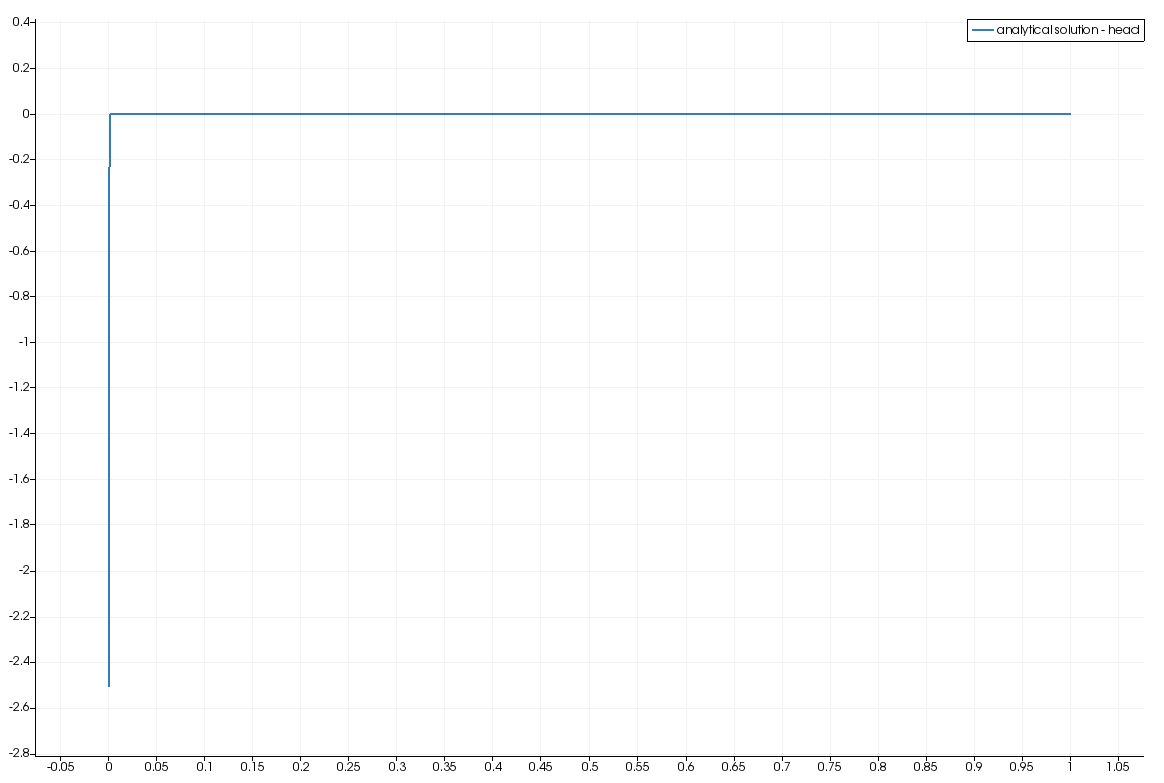
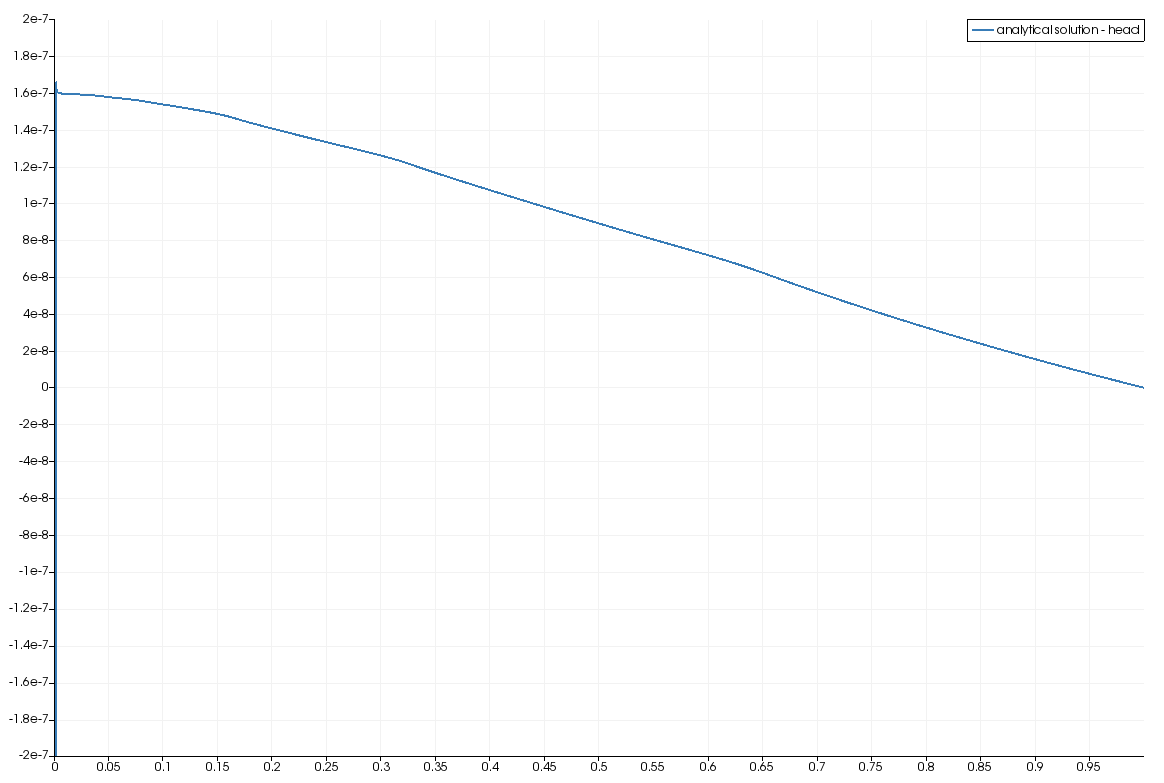
This article was written by Thomas Fischer. If you are missing something or you find an error please let us know.
Generated with Hugo 0.122.0
in CI job 545140
|
Last revision: February 26, 2025
Commit: [PCS] Avoid to compute the analytic block in ed9789e
| Edit this page on