Saturated Mass Transport

Overview

These benchmark compile a number of simple, synthetic setups to test different processes of saturated component transport of a solute.

The development of the equation system is given in this PDF. In the following, we present the different setups. The benchmark source files can be found in Parabolic/ComponentTransport/SimpleSynthetics.

Problem description

We use quadratic mesh with $0 < x < 1$ and $0 < y < 1$ and a resolution of 32 x 32 quad elements with edge length $0.03125 m$. The domain material is homogeneous and anisotropic. Porosity is $0.2$, storativity is $10^{-5}$, intrinsic permeability is $1.239 \cdot 10^{-7} m^2$, dynamic viscosity is $10^{-3} Pa \cdot s$, fluid density is $1 kg\cdot m^{-3}$, molecular diffusion is $10^{-5} m^2\cdot s^{-1}$. If not stated otherwise, retardation coefficient is set to $R=1$, relation between concentration and density is $\beta_c = 0$, decay rate is $\theta = 0$, and dispersivity is $\alpha = 0$.

Boundary conditions vary on the left side individually for each setup; right side is set as constant Dirichlet concentration $c=0$; top and bottom are no-flow for flow and component transport. Initial conditions are steady state for flow (for the equivalent boundary conditions respectively) and $c=0$.

Model setups

Diffusion only / Diffusion and Storage

Left side boundary conditions for these two setups are pressure $p=0$ and concentration $c=1$. The Diffusion only setup results in the final state of the Diffusion and Storage setup. For the former, retardation is set to $R=0$, while for the latter, $R=1$.

• The Diffusion only project file
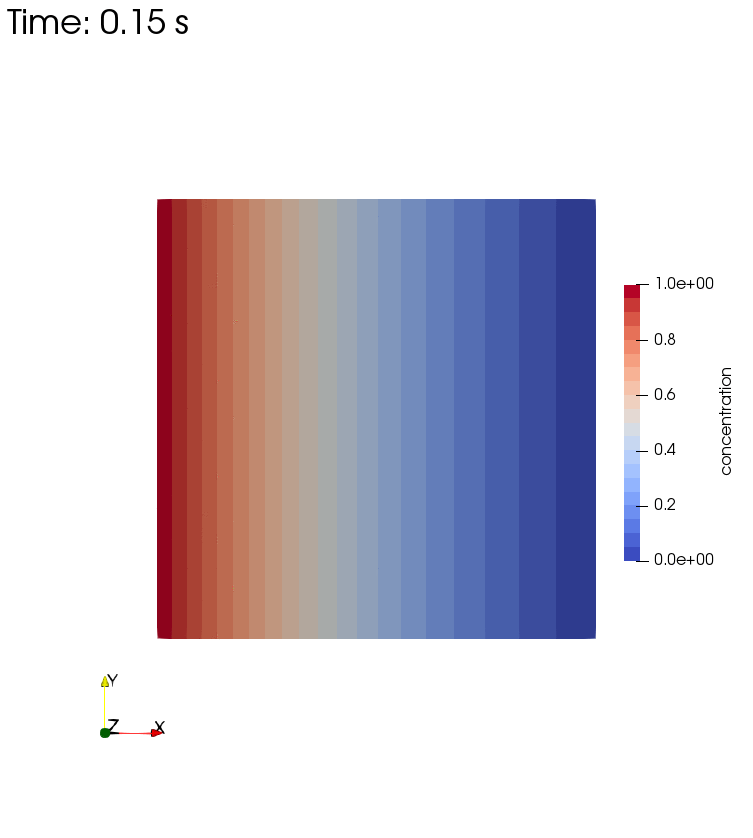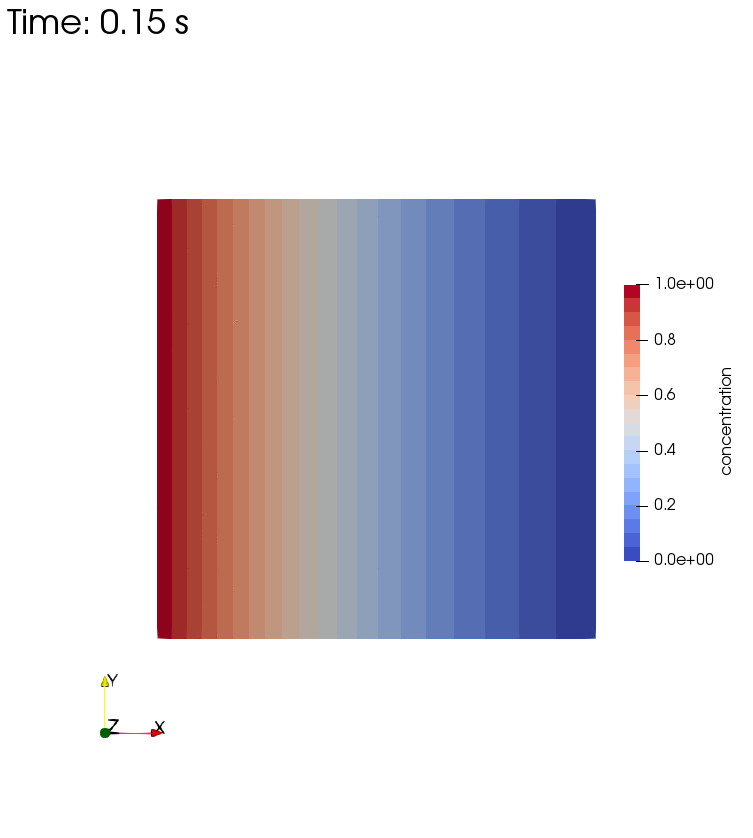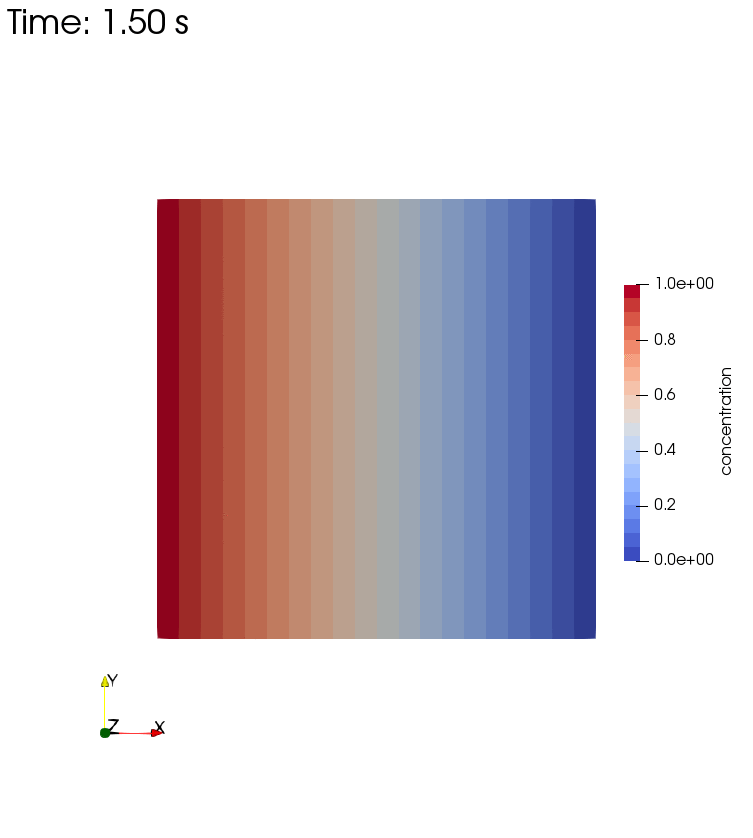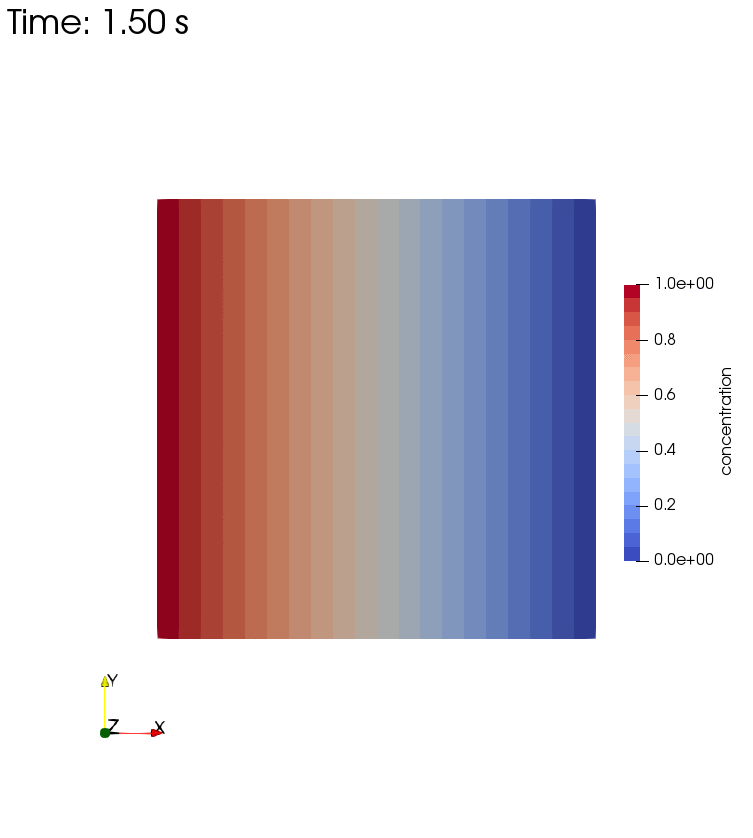
• The Diffusion and Storage project file

Diffusion, Storage, and Advection

Left side boundary conditions for this setup are pressure $p=1$ and concentration $c=1$.

• The Diffusion, Storage, and Advection project file

Diffusion, Storage, Advection, and Dispersion

Left side boundary conditions for these setups are pressure $p=1$ and concentration $c=1$. The latter is once given over the full left side, and in a second setup over half of the left side. Longitudinal and transverse dispersivity is $\alpha_l = 1 m$ and $\alpha_t = 0.1 m$.

• The Diffusion, Storage, Advection, and Dispersion project file
• The Diffusion, Storage, Advection, and Dispersion Half project file

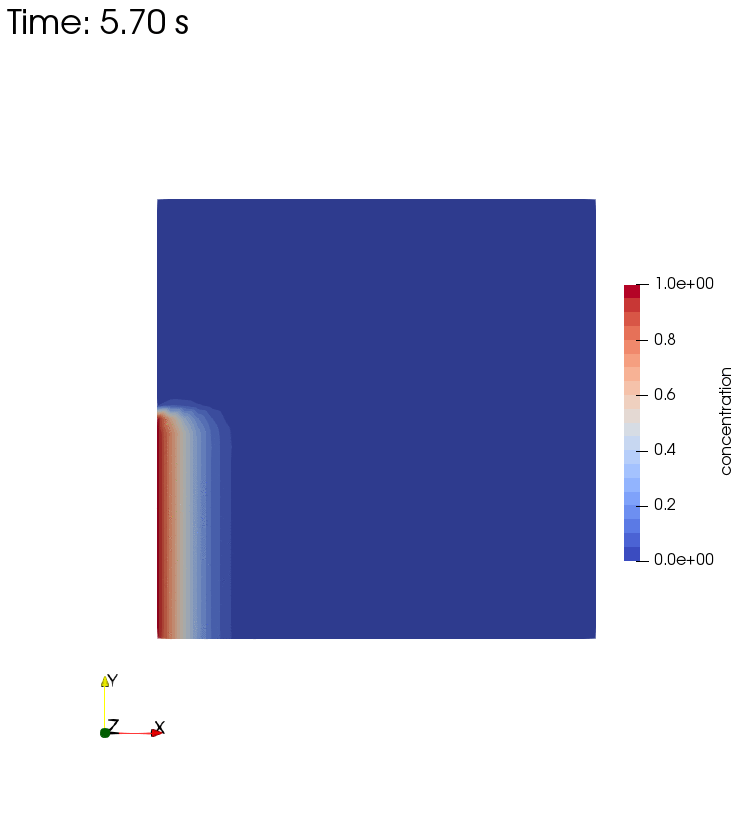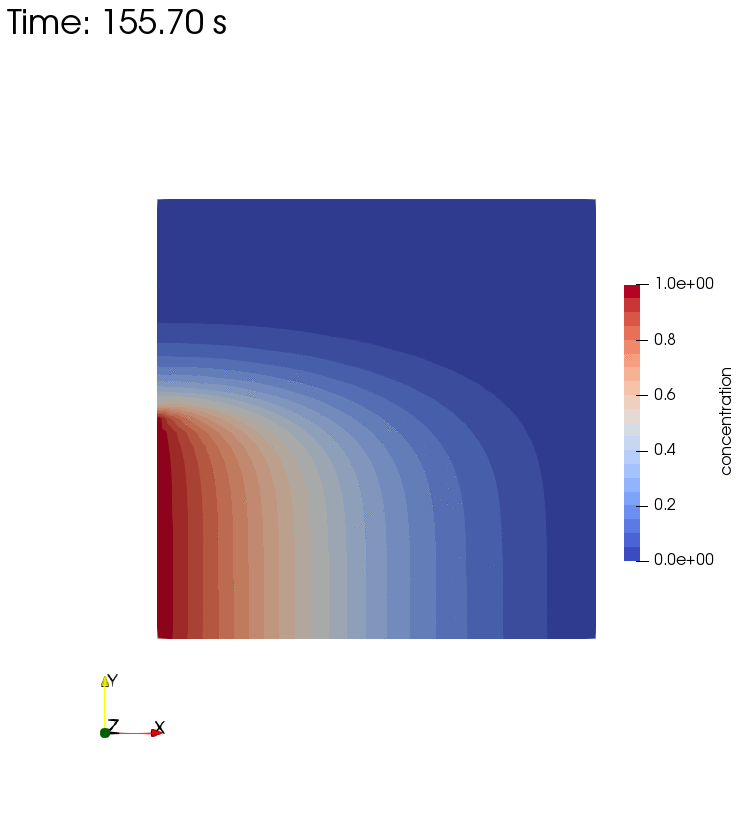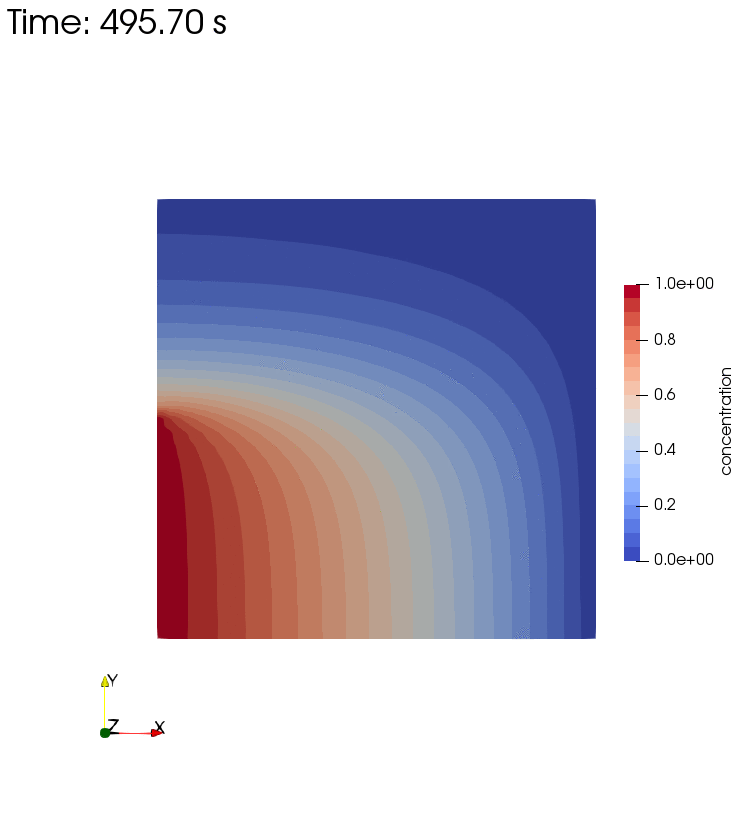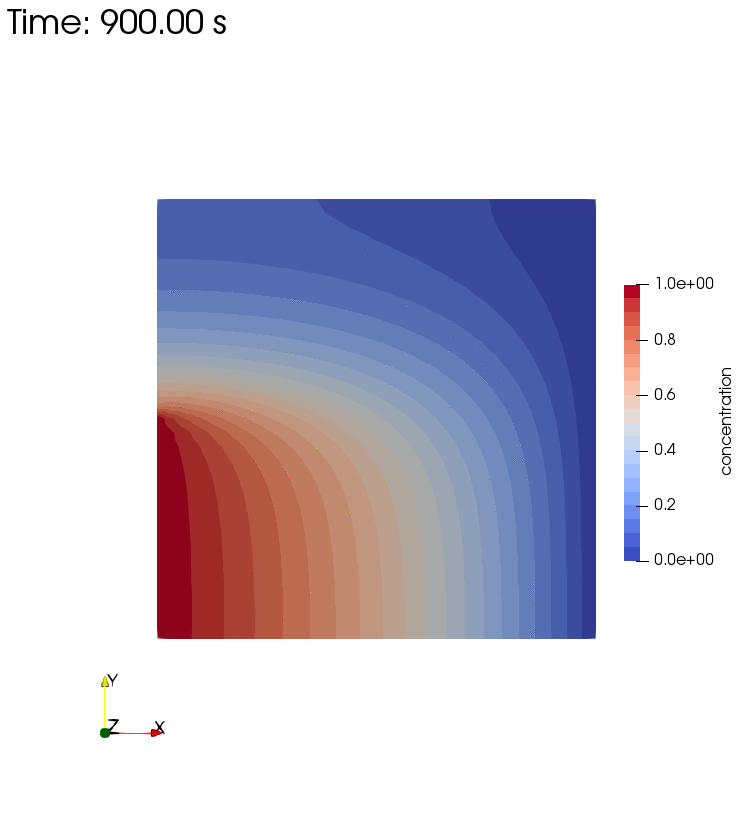
Diffusion, Storage, Gravity, and Dispersion

Boundary condition for this setup is pressure $p=0$ for the top left corner and concentration $c=1$ for half of the left side. Relation between concentration and gravity is $\beta_c = 1$.

• The Diffusion, Storage, Gravity, and Dispersion project file

Diffusion, Storage, Advection, and Decay

Left side boundary conditions for this setup are pressure $p=1$ and concentration $c=1$. Decay rate is $\theta = 0.001 s^{-1}$.

• The Diffusion, Storage, Advection, and Decay project file

Changes With Inclusion of Non Boussinesq-Effects

The changes to the original setup are described in this PDF.